Vlad Grechyshkin

Vlad Grechyshkin

Published in 3D, Three.js · · 4 min read

A practical introduction to half-edges in Three.js

Mesh processing applications often require accessing specific vertices, edges or faces. Depending on the programming language and framework used, these values might not be tailored for such operations. This blog post aims to highlight the benefits of a half-edge data structure when developing said applications in Three.js.

What are half-edges?

A half-edge is a directed line segment that goes from one vertex to another, like an arc in graph theory. This means that, in a triangle mesh, each edge is composed of two oppositely oriented half-edges.

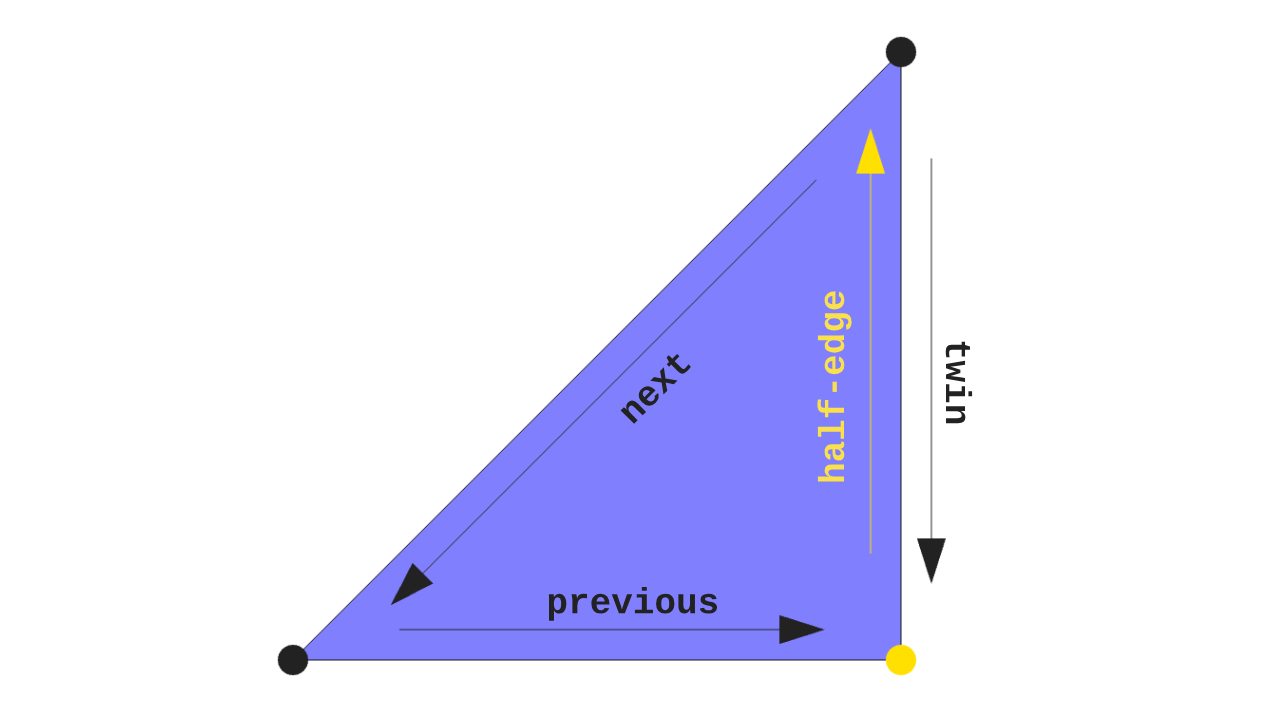
half-edge example

Each half-edge belongs to one side of the edge and has a reference to the opposite one, commonly referred to as its twin or pair. It also has a reference to the next half-edge along the same side, as well as its face and either incident vertex.

Depending on the implementation, it can also include a reference to its previous half-edge. Contrarily, each vertex and face only know, if any, about one of their half-edges, chosen arbitrarily.

Why use them?

A Three.js BufferGeometry uses a face-list representation to describe a mesh. Whether indexed or not, this representation is optimised for rendering and storage, not complex querying.

For example, consider finding whether two vertices share an edge. To do so, one would have to iterate each face and check if both vertices belong to it:

// using an indexed geometry for mental sanity
const indices = geometry.index.array

// vertex indices to check
const v0 = 0
const v1 = 1

// iterate all faces
for (let i = 0, n = indices.length; i < n; i += 3) {
  // get each face vertex index
  const a = indices[i]
  const b = indices[i + 1]
  const c = indices[i + 2]
  const face = [a, b, c]

  // check if both vertices are in the same face
  if (face.includes(v0) && face.includes(v1)) {
    // do something
    console.log('v0 and v1 are connected!')
    break
  }
}

Using half-edges, this operation can be simplified to checking if any of the half-edges of one vertex belong to the other vertex.

// suppose `struct` is an initialized half-edge data structure
const v0 = struct.vertices[0]
const v1 = struct.vertices[1]

let halfedge = v0.halfedge
do {
  // check if the current half-edge in the loop is connected
  if (halfedge.twin.vertex === v1) {
    // do something
    console.log('v0 and v1 are connected!')
    break
  }

  // loop around v0 in a clockwise direction..
  halfedge = halfedge.twin.next
  // ...until the starting half-edge is reached
} while (halfedge !== v0.halfedge)

This way, the time complexity improves from O(n) where n is the number of faces to O(m) where m is the number of faces connected to the queried vertex. Moreover, the connectivity becomes inherent to the structure and removes the need of explicitly storing values that may not be reusable in other operations.

A practical example

The previous search code block hints towards solving a common mesh connectivity problem: finding the one-ring neighborhood of a vertex. Instead of building a set of neighboring vertices for each vertex by iterating all faces, loop the half-edges of a vertex in either direction to find its neighbors:

function * getNeighbors (vertex) {
  let halfedge = vertex.halfedge
  const start = halfedge
  do {
    yield halfedge.twin.vertex
    halfedge = halfedge.twin.next
  } while (start !== halfedge)
  return null
}

The following code snippet uses three-mesh-halfedge and getNeighbors() on a simple hexagonal mesh to visualize the neighbors of its center vertex:

Each time the button is pressed, the next neighbor and related half-edges in a clockwise direction are highlighted. This operation may seem inconsequential, but it is used in numerous significant processes, such as mesh smoothing, decimation or subdivision.

To exemplify, here is another snippet using the previous code to implement a simple Laplacian smoothing algorithm:

Pressing the “smooth” button updates the position of each vertex to the average position of its neighbors. Using the getNeighbors() function, their positions become directly accessible.

Conclusion

A half-edge data structure offers a simple yet robust solution to overcoming the limitations of a face-list representation. It allows for better mesh navigation, which in turn reduces both complexity and implementation effort.

Of course, this solution does not come for free; building a half-edge data structure requires additional time and memory. However, given the average complexity of mesh processing applications, the cost is typically worthwhile.

Therefore, consider using this structure if your application requires accessing specific mesh values and information to implement expensive operations.

Resources

Here are some posts and in-depth explanations that may be helpful when dealing with half-edges:

Have fun!